What you need to know... solving the Rosetta Code's 'circles of given radius through two points' problem
No long time ago I was visiting the Freecodecamp forum to see how I could help. Then I found a question that took my attention.
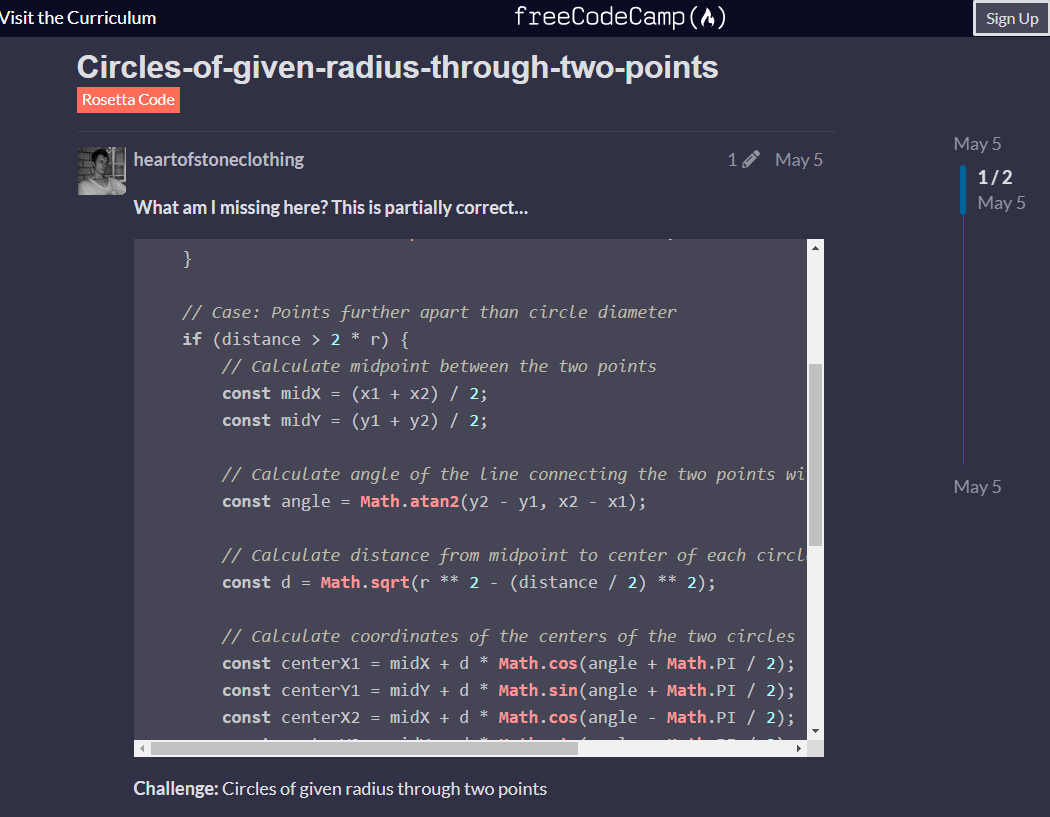
The question was one of the many code problems listed in a section of the Freecodecamp curriculum to practice for code interviews. Specifically, the question was one under the Rosetta Code problems.
Freecodecamp provides an interface to Freecodecamp students to try some Rosetta Code exercises. For example, here it is the presentation of our concerning exercise on the Freecodecamp site.
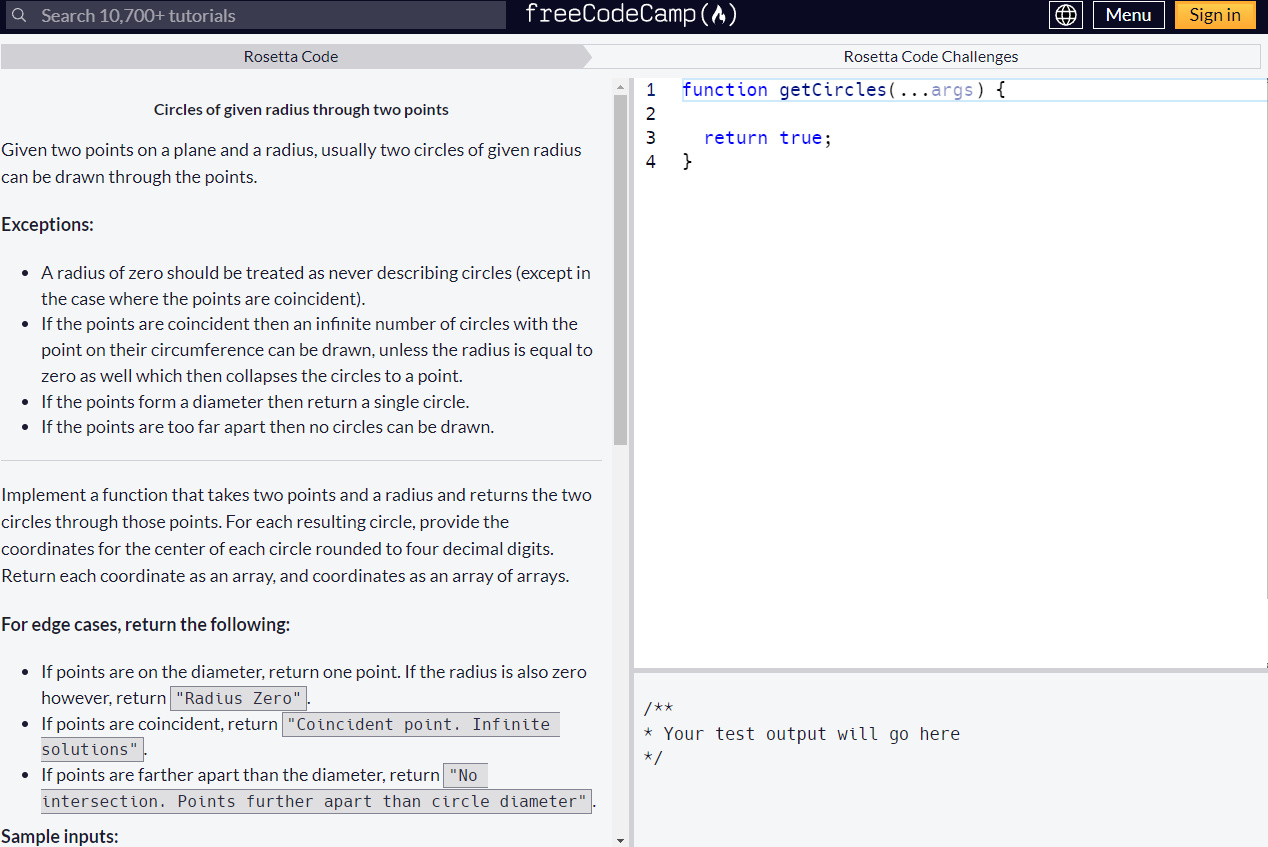
But the Rosetta Code project is actually a different project to Freecodecamp. It is in fact a collection of problems for coding practice and examples. Contributors to the Rosetta Code are asked to post exercises as well as to suggest solutions in different programming languages.
For example: This was the solution given in Javascript by the time of this writing to our concerning exercise:
const hDist = (p1, p2) => Math.hypot(...p1.map((e, i) => e - p2[i])) / 2;
const pAng = (p1, p2) => Math.atan(p1.map((e, i) => e - p2[i]).reduce((p, c) => c / p, 1));
const solveF = (p, r) => t => [r*Math.cos(t) + p[0], r*Math.sin(t) + p[1]];
const diamPoints = (p1, p2) => p1.map((e, i) => e + (p2[i] - e) / 2);
const findC = (...args) => {
const [p1, p2, s] = args;
const solve = solveF(p1, s);
const halfDist = hDist(p1, p2);
let msg = `p1: ${p1}, p2: ${p2}, r:${s} Result: `;
switch (Math.sign(s - halfDist)) {
case 0:
msg += s ? `Points on diameter. Circle at: ${diamPoints(p1, p2)}` :
'Radius Zero';
break;
case 1:
if (!halfDist) {
msg += 'Coincident point. Infinite solutions';
}
else {
let theta = pAng(p1, p2);
let theta2 = Math.acos(halfDist / s);
[1, -1].map(e => solve(theta + e * theta2)).forEach(
e => msg += `Circle at ${e} `);
}
break;
case -1:
msg += 'No intersection. Points further apart than circle diameter';
break;
}
return msg;
};
There was no much follow up in the Freecodecamp thread after all, but I still wanted to check the problem and the code on the Rosetta Code page, only to find some possible errors in the code.
Keep in mind that the current Rosetta Code solution can be eventually updated
This motivated me to revise the problem.
At the same time, I wanted for a while to test the use of d3.js and scrollama.js for storytelling, and this problem seemed like a good opportunity to give it a go.
So what not to combine those two interests and to make an animation of few things we should know to get a solution of the Rosetta Code problem?
Notice that I won’t provide any code here: I will only show some theory that could help to solve it. I will end this post with a short discussion about my findings and how they compare to the posted Rosetta Code solution, and a bit of the technologies I used for this post too.
So… Let’s get this started!
In Action
Let's draw two points, A and B at any place of a cartesian plane, each defined by their (x,y) coordinates, being d > 0 the distance between those two points.
Let's start simple by assigning the same y-coordinate to both points.
Now let's draw a segment between our points A and B. Let's call it the segment AB
A circle could be defined as "all the points from the same distance known as the radius to a point called the center". That means that in order for our points A and B to be part of a circle, they have to be at a distance of radius r to the center of that circle.
Under the previously stated conditions, how many circles would contain our two points if we don't specify a radius?
Here one example: a circle of radius equal to the half length of the segment AB, with the middle point M of segment AB as the center of the circle.
There are other circles. Let's see some!
In fact, we can draw infinite number of circles as long as their radii are equal or larger than the half distance between A and B.
Notice that all the circles touch our two points while their centers get further away from our point M.
And there are more: we can include the circles in the opposite direction too.
All those circles form a family of circles containing our points A and B.
One peculiarity of this circle family is that their centers are colinear: they all belong to the perpendicular to the segment AB that passes through the middle point M.
Now, the exercise gives us two points and a radius. We have already spoken about the points. Let's say we got a radius corresponding to the following circles...
... but because we still don't know the coordinates of their centers we are not able to provide a numeric (programmatic) solution for them :(.
So another way to pose part of our problem would be: How do we code a script that calculates the cooordinates of the centers of any of the circles of the corresponding circle family, given a radius and the two points?
Let's see what we have so far. The two points and the radius are given. We have also learned that the centers are colinear to the perpendicular that passes through the middle point M.
Let's select the point A and let's draw some useful data: the length of segment AM and the radius r, pointing to one of the possible centers.
I hope you will agree with me that the shape we have highlighted ressembles a side and hypotenuse of a rectangular triangle, which allows us to find a solution for the distance between M and one of the centers using Pitagoras. Let's call one of those centers C.
This is a bunch of good information! But it is not enough: we still need to translate that information into the xy-coordinates of the centers.
For the simple case where the AB segment is parallel to the the x-coord as our current example, finding the right coordinates of the centers would consist of simple additions and substractions to the coordinates of the point M. The challenge of a more general solution lies on the fact that points A and B can be wherever in our plane. For example, let's say we had a different point A.
This is a rotation of the geometry! Here we won't get the right solution by simply adding or substracting to the point M. We need to find the projection of the segment MC over the x and y axes of our cartesian plane. And that requires some trigonometry.
Those segments, dx and dy should be calculated based on the angle between the segment MC and the x-axis. In our example, that angle would be...
... the one indicated by the orange arc. It is the arctan of the perpendicular to the segment AB.
dx is the cosine of the angle by the length of the segment MC, and dy is similar but by using the sine.
Once you have the lengths of dx and dy, you have to add / substract them to the corresponding coordinates of the point M to get the coordinates of the centers of the circles. For example, here it is one of the circles after a addition...
And that's it!
Tada!
For my implementation, the angle of the perpendicular to AB was igual to:
angle = arctan( - (xB - xA)/(yB - yA) )
Then it was a question of trying different points to test the implementation. But there are a few things I had to keep in mind with my implementation that I would like to share…
So… What did we learn from this code?
First of all, the solution to this problem would be affected by the selection of the point, A or B, used as reference for further calculations.
In my case I used the point A as reference, but it is important to consider that I always left the point A to the left of the point B, by sorting them by their x coordinates. This is relevant.
The other thing I did was to use the middle point of the segment AB as my reference to find the centers of the circles. Why? Because it is equidistant to each of the centers. That is because the point M is not only the middle point between A and B but also between the centers of the any of the circles with the same radii. Selecting the middle point in this case makes the caculations easier.
Final Remarks
How my approach was different to the one given in the solution found in the Rosetta Code page?
Well, first of all, I mentioned the relevance of the order of the reference points. The solution in the Rosetta Code page is not taking that in consideration, so you might have different results if you invert the order of the points.
What also makes the Rosetta Code solution a bit tricky is that the reference point used to calculate the centers seems to be the first point of entry (p1 in that code), which also makes more difficult the calculation of the necessary angles and coordinates. Bear in mind that the approach was not per se wrong: it is only more difficult and prone to error.
But it is up to you to try this or other approaches! There are many ways to approach this problem. Mine might be also incomplete, or even wrong. My invitation is for you to evaluate the existing one to this date (jul-2024) and see if you can improve that! I’m sure you can. I wish you happy coding!
Interested in my first experience working with d3.js, scrollama.js but also Jest for unit testing and Jekyll? Check this post to know more